【簡単】分散分析とは何かについてわかりやすく解説
分散分析についてわかりやすく解説している記事がなかなか見当たらなかったので、機械学習エンジニアでもある僕が記事を書いてみました。わかりやすく解説したつもりなので、最後まで読んで頂けると嬉しいです。
分散分析とは何か
分散分析とは、3種類以上の母集団のうち、少なくとも1つの組み合わせにおいて平均値に有意差(=意味のある差)があるかどうかを調べる方法となります。ちなみに、2つの母集団の平均値に有意差があるかを調べるだけであればt検定という手法を用います。
分散分析は文字だけだとイメージしにくいと思うので、図も用意しました。以下の図は3つの母集団の分布を表しています。
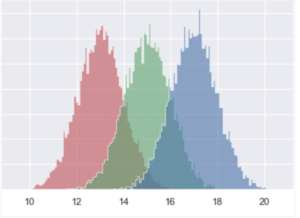
※例えば3種類の天気(雨、曇り、晴れ)において、横軸をその日のジュースの売上(万円)、縦軸をその日数(日)としていると考えていただくとイメージがわきやすいかと思います。
これら3つの母集団の平均値(こちらの図の場合はそれぞれ13, 15, 17あたり)に有意義な差があるかどうか調べるのが分散分析です。パッと見で有意差があると判断できそうですが、統計学的に判断を下すためには分散分析が必要です。
ちなみに分散分析という名前が付いているのは、実施する際に分散を用いるためです。ただし、あくまでも調べるのは「それぞれの母集団の平均値に有意差があるかどうか」なので要注意です。ややこしいですね。
分散分析の流れ
分散分析の流れは以下のとおりです。なお、詳細については後述するので、ここでは大まかな流れを捉えて頂ければ大丈夫です。
- 帰無仮説と対立仮説を立てる
- 有意水準を決める
- 各母集団から標本を取ってくる
- 標本を使ってF比を計算する
- 帰無仮説を元に計算したF比がF分布の棄却域に入っているか判定する
- 結論を下す
とりあえずざっくりとした流れを説明しましたが、専門用語が多く抽象的な説明でわかりにくいかと思います。以降で具体例を用いて丁寧に解説していきます。
具体例で実践
今回の例では、晴れ、曇り、雨の3つの天気において、1日のジュースの売上の平均値が優位に異なるのかどうかを検証していきます。ここでは母集団A~Cを以下のように定義します。
母集団A:晴れの日のジュースの売上
母集団B:曇りの日のジュースの売上
母集団C:雨の日のジュースの売上
さて、母集団の設定ができたところで、先ほどの流れに従って分散分析を実施していきます。
1. 帰無仮説と対立仮説を立てる
帰無仮説とは名前の通り「無に返したい仮説」つまり「棄却(=否定)したい仮説」のことです。今回の場合は、「3種類の母集団のうち、どの組み合わせにおいても平均値の有意差がない」が帰無仮説となります。
一方、対立仮説というのは「証明したい仮説」つまり今回の場合は「3種類の母集団のうち、少なくとも1つの組み合わせにおいて平均値に有意差がある」が対立仮説となります。まとめると以下のようになります。
帰無仮説:「3種類の母集団のうち、どの組み合わせにおいても平均値の有意差がない。」
対立仮説:「3種類の母集団のうち、少なくとも1つの組み合わせにおいて平均値に有意差がある。」
2. 有意水準を決める
有意水準とは「帰無仮説を棄却する基準」のことです。よく用いられる値としては有意水準5%や1%などの値があります。どのように有意水準を使うかは後ほど解説します。
ここでは「帰無仮説を棄却できるかどうかをこの値によって判断するんだな」くらいに思っておいてください。今回は有意水準5%とします。
3. 各母集団から標本を取ってくる
ここでは、それぞれの母集団からサンプルサイズ5で1回のみサンプリングすることにします。以下をサンプリングしたデータとします。
母集団Aから取り出したサンプル:17, 20, 18, 17, 15
母集団Bから取り出したサンプル:14, 12, 15, 12, 16
母集団Cから取り出したサンプル:11, 13, 9, 10, 11
4. 標本を使ってF比を計算する
■F比とは
まずF比とは何かについて説明します。F比とは、以下の式で計算される統計量のことです。
F比 = 効果の分散 / 誤差の分散
「効果」や「誤差」の意味については後ほどご説明しますが、ここで重要なのは、このF比という統計量がF分布というすでによく調べ上げられた分布に従っているということです。
ここでF分布を見てみると、以下のような感じです。(後ほど触れますが、F分布は自由度によって概形が少し変わります。)
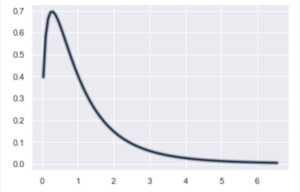
重要なのは、帰無仮説のもとで計算したF比の値によって、レアなことが起きているのかどうかがわかるので、帰無仮説が棄却できるかどうかを判断できるということです。
もう少し簡単に言うと、あまりにも大きいF比が計算結果として出れば「最初に立てた仮説そのものが間違ってるんじゃね?」ってことです。
例えば、有意水準を5%とした場合、棄却域の境目の部分のF比は、F分布表より5.2などとわかるので、帰無仮説を元に計算したF比(例えば6.5などの値)が5.2よりも大きい場合はレアなことが起きていると判断し、帰無仮説を棄却できるわけですね。
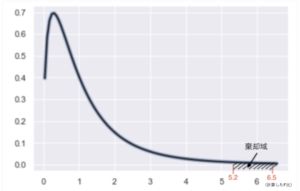
■効果や誤差とは
さて、F比の使い方がなんとなくわかったところで、次は効果や誤差とは何かについて説明していきます。効果や誤差については以下の図を見るとわかりやすいかと思います。
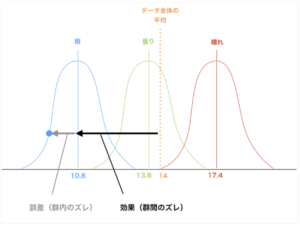
ここで、図中の1つのデータ(青丸)について考えます。このデータはデータ全体の平均値から矢印の分だけズレていますね。
このズレは、「データ全体と雨の日のズレ」と「雨の日の平均からのズレ」の2つに分解して考えることができます。
ここで、前者のズレを効果(=郡間のズレ)、後者のズレを誤差(=群内のズレ)と呼びます。
原理としては、F比というのはこの効果のズレと誤差のズレの比を表しており、F比が大きいということは
効果のズレ > 誤差のズレ
がより顕著であることを意味しています。これはすなわち、それぞれの群の平均がデータ全体の平均から大きくズレていることになります。
■F比の計算
さて、効果や誤差についてもなんとなく理解できたところで、いよいよF比の計算に入っていきます。
①サンプルごとの平均とデータ全体の平均を計算
まずはサンプルごとの平均を計算していきます。おさらいすると、取り出したサンプルは以下なので、
母集団Aから取り出したサンプル:17, 20, 18, 17, 15
母集団Bから取り出したサンプル:14, 12, 15, 12, 16
母集団Cから取り出したサンプル:11, 13, 9, 10, 11
それぞれの平均は、
サンプルAの平均 = (17 + 20 + 18 + 17 + 15) / 5
= 17.4
サンプルBの平均 = (14 + 12 + 15 + 12 + 16) / 5
= 13.8
サンプルCの平均 = (11 + 13 + 9 + 10 + 11) / 5
= 10.8
となります。
また、データ全体の平均は
データ全体の平均 = (17.4 + 13.8 + 10.8) / 3
= 14
となります。
②効果の平方和と誤差の平方和を計算
効果の平方和を出すためには、各群の平方和(それぞれの群の平均がデータ全体の平均からどれだけズレているか)を求める必要があります。
各群の平方和は、
各群の平方和 = (各郡の平均 – データ全体の平均)^2 * サンプルサイズ
なので、
Aの群の平方和 = (17.4 – 14)^2 * 5
= 57.8Bの群の平方和 = (13.8 – 14)^2 * 5
= 0.2Cの群の平方和 = (10.8 – 14)^2 * 5
= 51.2
となります。
その総和である効果の平方和は
効果の平方和 = Aの群の平方和 + Bの群の平方和 + Cの群の平方和
で表されるので、
効果の平方和 = 57.8 + 0.2 + 51.2
= 109.2
となります。
また、誤差の平方和は、
誤差の平方和 = (個々のデータ – データ全体の平均)^2 の総和
なので、
誤差の平方和 = (17 – 17.4)^2 + (20 – 17.4)^2 + … + (15 – 17.4)^2 +
(14 – 13.8)^2 + (12 – 13.8)^2 + … + (16 – 13.8)^2 +
(11 – 10.8)^2 + (13 – 10.8)^2 + … + (11 – 10.8)^2
= 109.19
となります。(効果の平方和と誤差の平方和がたまたまほぼ同じになってしまいました。)
③自由度を計算
自由度の計算は突き詰めるとなかなか難しいところなので、ここでは「とりあえずこうなるんだな」という程度の理解で大丈夫です。あくまでも最重要の目的は分散分析を実施することになるので、数学的な意味合いについては余裕があれば調べてみてください。
全体の自由度 = データ全体のサンプルサイズ -1
効果の自由度 = 群の数 -1
誤差の自由度 = 全体の自由度 – 効果の自由度
なので、
全体の自由度 = 15 – 1
= 14
効果の自由度 = 3 -1
= 2
誤差の自由度 = 14 – 2
= 12
となります。②で求めた平方和と③で求めた自由度より、効果の分散と誤差の分散を計算していきます。
④効果の分散と誤差の分散を計算
効果の分散 = 効果の平方和 / 効果の自由度
誤差の分散 = 誤差の平方和 / 誤差の自由度
なので
効果の分散 = 109.2 / 2
= 54.6
誤差の分散 = 109.19 / 12
= 9.1
⑤F比を計算
先ほど説明したとおり、
F比 = 効果の分散 / 誤差の分散
なので、
F比 = 54.6 / 9.1
= 6.0
となります。かなり大変でしたが、やっとF比を計算することができました。
5. 帰無仮説を元に計算したF比がF分布の棄却域に入っているか判定する
今回は効果の自由度2、誤差の自由度12のF分布について考えます。このとき、こちらのF分布表より有意水準5%のF比は3.89となります。
ゆえに、先ほどのF分布の説明でご覧頂いた図のように、帰無仮説のもとで計算したF比(=6.0)が棄却域の中に入っています。
6. 結論を下す
よって、「5%以下でしか起こり得ないレアなことが起きている」と判断し、帰無仮説を棄却することができます。結論としては「3種類の母集団のうち、少なくとも1つの組み合わせにおいて平均値に優位差がある。」になります。以上です。長かったですが、分散分析お疲れ様でした!
最後に
最後まで読んで頂き、ありがとうございました。一度で理解するのはなかなか大変だと思うので、何回かに渡ってじっくり読んで頂ければと思います。
なお、ここで実施した分散分析は一元分散分析というものになります。
参考
書籍
分散分析について理解する上で、こちらの書籍が非常にわかりやすかったです。
スクール
こちらのスクールでは分散分析についても学ぶことができます。
テックアカデミー(データサイエンスコース)
![]()
また、僕の運営しているオンライン型プログラミングスクールCodeCafeでも、Pythonを教えていますので、気になる方は以下をご覧ください。
» プログラミングスクール CodeCafeの詳細はこちら


