2021/05/29 (更新日: 2022/08/12)

【簡単】t検定とは何かわかりやすく解説【統計の基礎をpythonエンジニアが解説】

Programming

統計の勉強をし始めたばかりの頃に出てくるt検定って難しいですよね。聞きなれない専門用語が多く登場する上に、概念的にもなかなか掴みづらいです。

そこで、t検定に対する理解を深めて頂くために、本記事で分かりやすく解説しました。皆さんの学習の助けになれば幸いです。

【注意】
この記事では分かりやすいように1標本の場合を考えます。ただ、2標本のt検定についても基本的な流れはほぼ同じですので、こちらの記事を読んで頂くと2標本のt検定を学習する際にもイメージが掴みやすいかと思います。

t検定とは

t検定とは、「母集団の平均値を特定の値と比較したときに有意に異なるかどうかを統計的に判定する手法」です（1標本の場合）。母集団が正規分布に従い、かつ母分散が未知の場合に使う検定手法になります。

ちなみに、t値という統計量を用いて行うのでt検定と言います。

t検定の流れ

t検定の流れは以下のとおりです。

帰無仮説と対立仮説を立てる
有意水準を決める
各母集団から標本を取ってくる
標本を使ってt値を計算する
帰無仮説を元に計算したt値がt分布の棄却域に入っているか判定する
結論を下す

とりあえずざっくりとした流れを説明しましたが、専門用語が多く抽象的な説明でわかりにくいかと思います。以降で具体例を用いて丁寧に解説していきます。

具体例で実践

今回の例では、国内の成人男性の身長を母集団として考えます。このとき、「母平均が173cmよりも大きいかどうか」を検証していきます。それでは見ていきましょう。

1. 帰無仮説と対立仮説を立てる

帰無仮説とは名前の通り「無に返したい仮説」つまり「棄却（=否定）したい仮説」のことです。今回の場合は、「母平均は173cmと差がない」が帰無仮説となります。このようにまずは計算しやすい土台を作った上で計算を進めていき、矛盾が生じたところでこの仮定を棄却するわけですね。

対立仮説というのは「証明したい仮説」つまり今回の場合は「母平均が173cmよりも大きい」が対立仮説となります。まとめると以下のようになります。

帰無仮説：「母平均は173cmと差がない」
対立仮説：「母平均が173cmよりも大きい」

2. 有意水準を決める

有意水準とは「帰無仮説を棄却する基準」のことです。よく用いられる値としては有意水準5%や1%などの値があります。どのように有意水準を使うかは後ほど解説します。

ここでは「帰無仮説を棄却できるかどうかをこの値によって判断するんだな」くらいに思っておいてください。今回は有意水準5%とします。

3. 母集団から標本を取ってくる

ここでは、母集団からサンプルサイズ5で1回のみサンプリングすることにします。以下をサンプリングしたデータとします。

175, 172, 174, 178, 170

先に標本平均と標準誤差を計算しておきます。標準誤差というのは、標本平均の標準偏差のことです。これらは後ほどt値を計算する際に用います。

まず、標本平均を計算します。

標本平均 = (175 + 172 + 174 + 178 + 170) / 5
= 173.8

となりました。
次に、

標準誤差 = 標準偏差 / √データの個数

なので、まずは不偏分散を用いて標本の標準偏差を計算していきます。

標準偏差 = √[{(175-173.8)^2 + (172-173.8)^2 + … + (170-173.8)^2} / (5-1)]
= 3.03

となったので、

標準誤差 = 3.03 / √5
= 1.36

と標準誤差を計算できました。
まとめると、標本平均=173.8, 標準誤差=1.36となります。
次はt値の計算をしていきます。

4. 標本を使ってt値を計算する

■t値とは

まずt値とは何かについて説明します。t値とは、以下の式で計算される統計量のことです。

t値 = （標本平均 – 母平均）/ 標準誤差

計算の数学的な意味合いについてはすこし難しいので割愛しますが、重要なのはこのt値という統計量がt分布というすでによく調べ上げられた分布に従っているということです。

■t分布とは

t分布は正規分布に非常によく似た形をしています。正規分布とは違ってグラフの裾の部分が少し浮いているのが特徴です。以下は正規分布とt分布を比較したものになります。

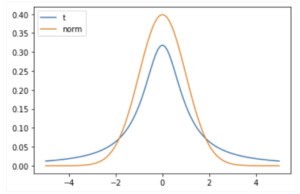
t分布はすでによく調べられているので、有意水準5%の点がどこかというのもt分布表や統計解析ツールを使えばすぐに分かります。

帰無仮説のもとで計算したt値の値によって、5%以下でしか起こらないレアなことが起きているのかどうかがわかるので、帰無仮説が棄却できるかどうかを判断できるというわけです。

もう少し簡単に言うと、あまりにも極端な値に偏ったt値が計算結果として出れば「最初に立てた仮説そのものが間違ってるんじゃね？」ってことです。

例えば、有意水準を5%とした場合、棄却域の境目の部分のt値は、t分布表より3.8などとわかるので、帰無仮説を元に計算したt値（例えば4.5などの値）が3.8よりも大きい場合は5%以下の確率でしか起こらないレアなことが起きていると判断し、帰無仮説を棄却できるわけですね。（以下の図は片側検定としています。）

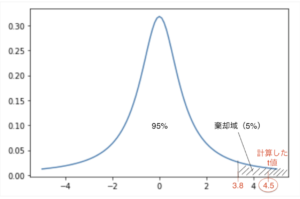
■t値の計算

さて、いよいよt値の計算に入っていきます。
おさらいすると、t値の計算式は、

t値 = （標本平均 – 母平均）/ 標準誤差

でしたね。
よって、

t値 = (173.8 – 173) / 1.36
= 0.59

となります。この値が棄却域に入っているかどうかを判定していきます。

5. 帰無仮説を元に計算したt値がt分布の棄却域に入っているか判定する

今回は自由度4（データの個数-1）のt分布について考えます。このとき、こちらのt分布表より有意水準5%のt値は2.77となります。

ゆえに、帰無仮説のもとで計算したt値（=0.59）は棄却域の中に入っていません。

6. 結論を下す

よって、「帰無仮説は棄却できない」と判断します。このときに注意しないといけないのが、帰無仮説が棄却できないからといって「母平均が173cmでない」とは限らない点です。あくまでも「立てた仮説が棄却できなかった。」つまり「母平均が173cmであると結論づけることはできなかった」いうことだけが言える点に注意してください。

ちなみにもし帰無仮説のもとで計算したt値が棄却域に入っていた場合は、帰無仮説が棄却できます。よってその場合、最終的な結論としては「母平均は173cmより大きい」となります。それではt検定お疲れ様でした！